How many decades will your IRA enjoy tax-free growth?
Posted on June 21, 2019

A possible change in tax law would cut the number years our IRAs that we leave to our children or other heirs will grow tax free. The change, described here, would require that our IRAs be fully distributed within ten years of our death. Under current law my IRA that I leave to an heir could easily exist for 30 years after I’ve died. Some part of my first contribution to my IRA in 1981 grows tax-free for 80 years! That part will have grown by 256X in real spending power. This post explains how under current tax law I get 80 years of tax-free growth on my first contribution to my IRA in 1981.
Last week I discussed the two basic advantages of IRAs.
• You get to play the game of different tax rates. A difference in your marginal tax rate 1) when you contribute and 2) at time you withdraw can mean you net more to spend than if the marginal rates were the same at both those times.
• Your IRA nets you more to spend than the alternative of keeping it invested in a taxable account because you are avoiding taxes – primarily capital gains taxes – for all the years your contribution is in your IRA. Each withdrawal from your IRA ends that tax-free run on that amount.
I calculate that tax-free growth is the greater benefit of the two, and I focus on this effect in this post. I’ll address the issue of marginal tax rates that heirs may pay from greater annual distributions (over 10 years vs. 30 or more years) – which seems to have alarm bells ringing for some – in the next post. The immediate question to answer:
• How do I get an 80-year run of tax-free growth on some part of my first contribution to my IRA in 1981 and what happens to it over time? We’ll follow what happened to that first contribution in 1981– the bottom layer in my total IRA – in this post. You’ll get the idea of what happens to all the other contributions.
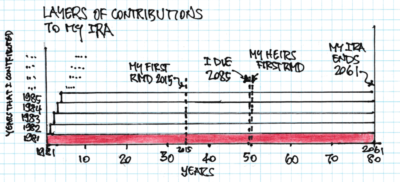
== My first 33 years of tax-free growth ==
I made my first contribution – $2,000 – to my Traditional IRA in 1981. My 1981 contribution grew tax-free for 33 years to 12-31-14 before I was first required to withdraw a part in 2015 for my Required minimum Distribution (RMD).
I know invested my 1981 contribution in a stock fund that returned no less than the index fund VFIAX – one of the few that existed in 1981. Using VFIAX as the measure, my $2,000 in 1981 was about $71,400 on 12-31-14. That’s a combination of real growth and inflation. Let’s drop inflation and state all future dollar values in the constant dollar spending power of 12-31-14.
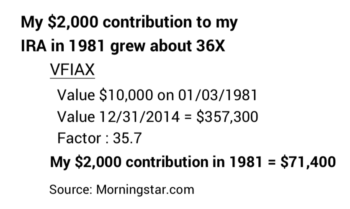
== RMD and the next 17 years ==
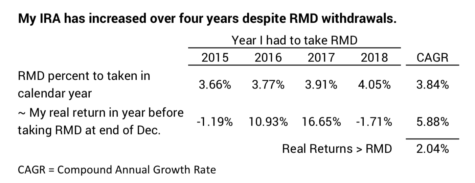
My first four years of RMD. My first RMD of 3.66% in 2015 was based on the value of my IRA on 12-31-14. My four RMD withdrawals have averaged about 3.8% per year. Real returns on my portfolio have averaged 5.9% per year. (If you follow the investment advice in Nest Egg Care, that also would have been your real return.) My portfolio has grown in real spending power by 2% per year and was 8% greater on 12-31-18. The $71,400 on 12-31-2014 increased in real spending power to $77,300 by 12-31-2018.
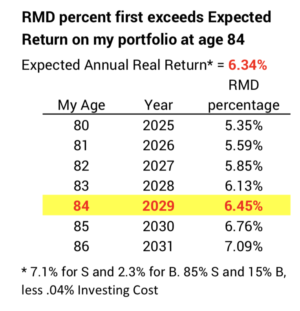
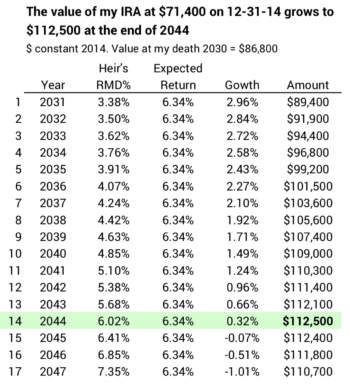
The balance of my lifetime. At expected return rates for stocks and bonds and my low investing cost, my IRA will continue to grow in real spending power for about the next ten years. I described this in this post: RMD percentages are less than the 6.34% expected real return rate for my portfolio through 2028. In 2029 – my age 84 – the 6.45% RMD percentage – first exceeds the expected return on my portfolio.
At the end of 2030 the value of the remaining part of my 1981 contribution to my IRA is $86,800 measured in 2014 spending power. That’s +20% from 12-31-14.

== The next 30 (or more) years ==
Let’s assume I name a non-spouse heir as beneficiary of my IRAs. I’m simplifying here; of course Patti is the first beneficiary of my IRA, but let’s assume I leave it to a non-spouse heir.
Assume I die at age 85 in 2030. My IRA passes to an heir age 55. My IRA is then subject to an RMD schedule that is different from my RMD schedule. Her RMD applies to both Roth and Traditional IRAs, ending the run of tax-free growth on the amount withdrawn.
In the first year she must withdraw based on her Life Expectancy Factor from that table: 29.6. That translates to an RMD of about 3.4% (1/29.6) in 2031. That’s about half the percentage I took the year before. Her RMD in future years calculates by subtracting 1 from her starting 29.6 Life Expectancy Factor. Her RMD percentage increases fairly steeply each year. It first exceeds the 6.34% expected return in 2045 when she is 69. My IRA is fully depleted in 2061, 80 years after its start.
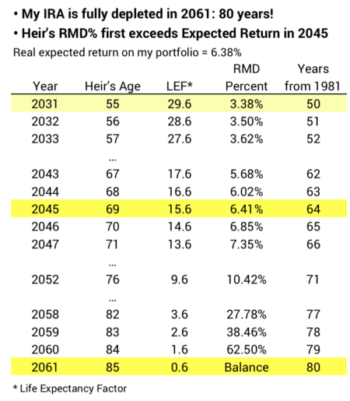
At expected returns my heir will see my IRA increase in real value to $112,100. That’s 57% more than on 12-31-14 – 30 years earlier. In this example, some part of my initial contribution has ridden 80 years tax-free growth at 7% annual returns: that’s eight doublings or real grown in spending power of 256X. Whew! All this from one $2,000 contribution in 1981!
If I left my IRAs to a younger heir, that heir would see more years of real growth in my IRA and my IRA would be depleted after 2061. If my heir was age 30 at my death, my IRA would run 55 years to 2086! A total of 105 years. That is more than ten doublings for some part of my initial $2,000: far more than 1024X in real spending power.
Conclusion: A possible change in tax law could limit the number of years that an IRA we leave to an heir can grow tax-free. An inherited IRA would have to be fully distributed within ten years. This post explains how under current law my IRA could exist 30 years or more (!) after my death and for a total of 80 or more years: a part of the $2,000 I contributed in 1981 grows tax-free for 80 years. At expected return rates some part of my initial contribution will increase in real spending power by a factor of 256X.