Think Real. Not Nominal. You’ll understand more clearly.
Posted on August 31, 2018

I always like to think of future financial returns in terms of inflation-adjusted dollars, generally called constant dollars. These are dollars stated in the same purchasing or spending power of some base year. Current dollars are the nominal count of the pieces of paper we call dollars. Because of inflation we need more current dollars to equate to the spending power of dollars from an earlier period. Stated differently, the spending power of our dollars shrinks over time due to inflation.

 

We understand more clearly when we just think real. The purpose of this post is to suggest you get in the habit of thinking real. Forget current dollars and nominal return rates.

 

Here’s an example of the math of adjusting dollars in one time period to the same purchasing power in another time period. I find how many 1984 dollars match the spending power of $4,000 dollars spent in 1977. I got the inflation factors for this calculation from here. The spending power of $6,840 in 1984 equals $4,000 in 1977.

 

 

Here’s the math to find the real investment return rate. It’s just not the simple addition of real + inflation = nominal. Or, real = nominal – inflation.

 

 

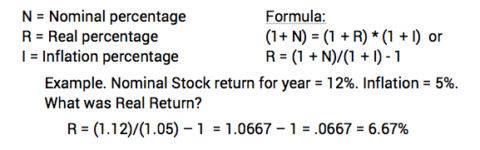
Here are some advantages to thinking Real and not Nominal:

 

• We make better financial decisions when we think in terms of real rates of return. I read an article recently that suggested we retirees should invest more into money market funds since rates have improved. That’s true, but my immediate reaction was, “Real money market rates are below 0% and have been for a couple of years. Why would anyone shift more to that?” You can see below that real money market rates are about -1.3% now, and that’s less than a year ago. (Note: I’m willing to accept a less than 0% real return at times. In December I’ll put all of our 2019 spending into money market or similar. I want to isolate my brain from the vagaries of the market.)

 

 

• We can get confused on how much we’ve really made (or lost) when we fail to state results in constant dollars. Patti and I purchased a lot for a second home many years ago. We paid $4,000 in 1977 as I recall. We eventually sold it for $8,000 in 1984. Did we come out ahead? No, not at all. We held it in a period of very high inflation: over 70% inflation in seven years. After the sales commission and taxes, we had an added 2,816 pieces of paper with $1 printed on them than we started with, but we lost real spending power!

 

 

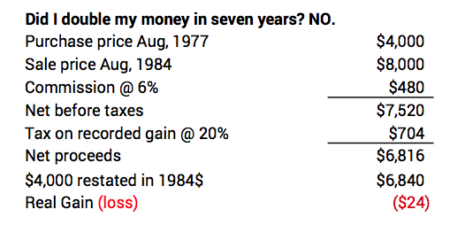
• We more clearly understand what a Retirement Withdrawal Calculator (RWC) tells us when we use real returns and constant-dollar portfolio values. I like FIRECalc because all returns are real returns and all and portfolio values are in constant spending power. We understand the results of our plan so more easily.

 

For the inputs that Patti and I chose for our plan in late 2014, FIRECalc shows the expected portfolio value in 19 years would be 70% more than our initial portfolio. Let’s assume in this example a starting portfolio balance of $1 million. The expected result of our plan would mean we could spend about $835,000 in today’s spending power over the years (19 * $44,000), and we’d still have 70% more in spending power than we started with. That adds up to more than $2.5 million for us. (Knowing that tells us we would not have to stick with that $44,000 spending amount for every year in the future.) Wow.

 

 

I like the Vanguard RWC, but I have no use for the numbers it displays for future portfolio values on its results graph. Those numbers include inflation, and because of the way Vanguard builds its sequence of returns, one can’t apply an inflation adjustment to understand what those numbers really mean. We don’t get close to understanding that our total spending power will be 2½ times the amount we start with if we ride a more average sequence of returns.

 

• We can do financial analysis more simply when we use constant dollars. In a week or so, I’ll post my analysis of whether you should take Social Security early (before age 70) or wait for the 8% boost you’d get by waiting one year. The conclusion is clear to me when I put all the numbers in constant dollars. But I read many articles that get the logic and math really confused, partly because they don’t use constant dollars and real return rates for the analysis.

 

 

Conclusion: We’ll all understand much more clearly when we think in terms of constant dollars (constant spending or purchasing power) and real return rates. Forget current dollars and nominal rates of return.