What’s the fundamental advantage of a Retirement Account?
Posted on June 14, 2019

Does it ever make sense to not add to your IRA when you have money saved that you won’t spend for many years? My friend Jim, years younger than I am, asked me, “I have money to invest. I don’t plan on spending it for many years. I’ve contributed to my IRAs for years, and I have a healthy amount now. I’m thinking I should stop putting more into my IRAs and that I should just keep it invested in my taxable account. Does this make sense?”
I used to be confused about this: I thought my Traditional IRA was converting what would otherwise be taxed as capital gains to income taxes. That is not correct. The answer – with one remote exception – is to ALWAYS put as much into Retirement Accounts as possible. You ALWAYS gain the fundamental advantage of a retirement account relative to a taxable account: you AVOID capital gains taxes on the growth of your investment for as long as you keep it in your IRA. The purpose of this post is to explain this fundamental advantage.
== Two types of IRAs are basically the same ==
Many folks are not clear on this, but as I mentioned in this post, a Roth IRA and Traditional IRA are essentially the same. You either pay income tax when you contribute (Roth IRA) or you avoid paying tax when you contribute but then pay the tax when you withdraw (Traditional IRA). You wind up with the exact same net amount from either type of IRA if your marginal tax rate when you contribute matches the marginal rate when you withdraw. This example shows that a $5,000 invested in a Roth IRA or a Traditional IRA net the exact same amount for spending.

== The game of different marginal tax brackets ==
The two don’t give the exact same spending power if the marginal tax rate when you contribute differs from the one when you withdraw. You play this game when you choose which kind of IRA to contribute to based on your view of the marginal tax rate when you (or your heirs) withdraw the money for spending.
• Roth over Traditional: You’d pick Roth if you are in a low marginal tax rate now and think you’ll be in a higher one when you withdraw it from your IRA for your spending. Example: your marginal tax rate now is 12%, and you withdraw it for spending when your are in the 22% bracket. You’ll win the game by paying income tax now at a 12% rate and not at a 22% rate.
• Traditional over Roth: You’d pick Traditional if you are in a high marginal tax bracket now and judge you will be in a lower one when you withdraw. Example: you’re in a 22% marginal bracket now and withdraw it for spending when you are in a 12% bracket. You’ll win the game by not paying 22% income tax now but paying 12% later.
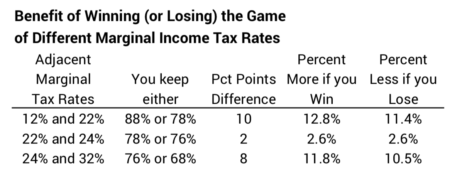
You don’t win much in this game if the differential in marginal tax bracket is small. If the current tax rate is 22% but is 24% in the future, Roth results in about 2.6% more to spend than Traditional.
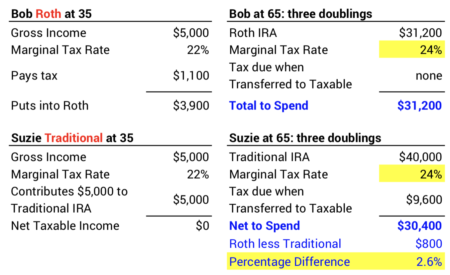
You win most when your marginal tax rates are very different when you contribute and when you withdraw. Using our current tax rates, the difference in adjacent marginal tax brackets could be 8 or 10 percentage points: 12% vs. 22%; 24% vs. 32%. Here’s a summary of what you might win (or lose) in this game:
== The 13% benefit from avoiding capital gains taxes ==
You ALWAYS win from IRAs because you AVOID capital gains tax on the growth of the amount you’ve invested and held for many years in your IRA.
To understand the benefit of avoiding capital gains taxes, I’m going going to exclude the game of different marginal tax brackets. I’m going to assume our player, Carl, nets the same from either Traditional or Roth when he withdraws. That makes it clearer to understand the benefit of avoiding capital gains tax: we calculate the capital gains tax effect as if we had invested in a Roth IRA. It’s the same effect as for a Traditional IRA, but it’s easier for our brains to understand the effect when our IRA is expressed as a Roth IRA.
Carl is 45. He has $2,000 – after paying his income taxes – that he can invest. He puts $1,000 in his taxable account to grow in the future. He puts $1,000 into his Roth IRA. He will hold these two accounts for 20 years and then sell the securities for his spending.
I’ll assume Carl invests solely in stocks with essentially zero investing cost (He’ll invest in an index fund.) and earns the expected 7.1% real return rate over two decades. That simplifies our math: we’ll consider that as two doublings or growth of a factor of four. I’ll assume Carl’s 7.1% growth in his taxable account is solely price appreciation. He only pays capital gains tax in the year he sells the stocks for his spending.
How much more does Carl have from his Roth IRA? Carl nets about 13% more for spending from his IRA than from his taxable account. This is the smallest advantage from an IRA than I can calculate, and it’s more than from winning the game of different marginal tax rates.

== It’s really more than 13% ==
I calculate that the benefit is greater than 13% more to spend with more years and different assumptions.
1) If I stretch the holding period to 30 years the benefit grows to 15%.
2) If Carl pays capital gains each year for 20 years on the 7% annual increase – not just in the 20th year on the total accumulated growth – he’d net over 20% more from the IRA. That nip of taxes on each year’s growth in his taxable account means there is less to compound.
3) The real capital gains tax rate is greater than 15% because the cost basis is not adjusted for inflation. The effect is that Carl pays capital gains tax on the inflation portion of any dollar gain. Example: even with no real growth in the value of his initial $1,000, Carl would record a taxable gain of +$600 on his initial $1,000 from inflation at 2.5% per year for 20 years. After paying the tax, he’d wind up with less spending power than he started with. I calculate the real capital gains tax rate is 17%, not 15%, for that 20 year period. That makes the benefit of the IRA about 15%.
4) The capital gains tax rate may be greater because of state taxes. I live in Pennsylvania. I pay 3% on capital gains. The total capital gains rate then is 18%. But I pay no tax on any withdrawals from IRAs.
== Avoid Capital Gains tax for many decades ==
I made my first contribution to my Traditional IRA in 1981, and it grew for 30 years before I withdrew any for our spending – I was first subject to RMD 34 years later in 2015. I’ll die with a balance in my IRA. My IRA is almost solely Traditional. RMD percentages will never deplete it. And I don’t have an incentive to withdraw more than RMD for our spending. Sales of securities from our taxable account will alway have the lowest tax cost and net more for us to spend (or gift) in our lifetimes.
== The one wrinkle for Jim to consider ==
If my friend Jim thinks his IRA is large now, it will only be larger in the future at expected returns for stocks and bonds. That means he may have a very large RMD in the future and fall into a higher marginal tax bracket. Jim could lose the game of different marginal tax rates.
Jim has a number of years for his current portfolio to grow before he takes his first RMD. As I discuss in this post, your RMD roughly doubles from age 70½ to age 83 at expected return rates. That’s because 1) the RMD percentage is less than the expected real return rate on your portfolio for all those years; that means the real value of your IRA will increase. And 2) the RMD percentage increases each year: by age 83 it’s about 70% greater than at age 70½ (6.13% vs. 3.65%). That large increase in RMD may mean a significant portion of income from his Traditional IRA is taxed at a high marginal rate: the jump from the current 24% marginal rate to the 32% rate is the biggest enemy.
Conclusion: You always want to invest as much as you can for retirement into your IRA. The fundamental benefit of an IRA is that you AVOID paying capital gains taxes on the growth of your portfolio for many years. I calculate that the 20-year benefit is about 15% more for you to spend by investing in your IRA as compared to the alternative of leaving it in your taxable account.
You also play the game of different marginal tax rates when you contribute to your IRA and when you withdraw from your IRA. You’d pick Roth IRA or Traditional IRA in this game. In some cases the decision as to which is best is clear. Many times it is not. The benefit of this game is secondary to the benefit of avoiding capital gains taxes.